1 目的
用于查找n个节点中,连通分支的数量。或者说是查找有多少个无交集的团体。并且可以很方便的查找每个个体是属于哪个连通分支的 特点:
- 每个分支是一种
树形的数据结构,但是方向是反的,是由子节点指向双亲节点 - 整个并查集是一个深林
- 用于处理
不相交集合的合并及查询问题 - 算法及其简单而高效
1.1 思想
给每个连通分支都选一个代表,分支里的全部节点都指向它。 所以要想知道两个节点是不是在一个分支里,比较他们分别指向的代表是不是一样的就好了。
合并两个连通分支也非常简单,让分支2的代表指向分支1的代表,这样分支1的代表也代表了分支2里面的全部节点。

2 主要操作
2.1 初始化
初始的时候,每个点都是只有一个元素的连通分支
int pre[1000];
2.2 查找
查找节点x是属于哪个连通分支的。就不停的在树中递归查找父节点,直到根节点
int find(int x)
{
int r=x; //委托 r 去找掌门
while(pre[r]!=r) //如果r的父节点不是r自己,则r不是根节点
r=pre[r] ; //递归
return r ;
}
2.3 合并
先判断x和y是不是在一棵树里,不是就让一棵树的根节点放在另一棵树的根节点下面
void join(int x,int y)
{
int fx=find(x),fy=find(y); //分别查找x和y的代表
if(fx!=fy)
pre[fy]=fx; //fx也成为了y所在分支的代表
}
3 路径压缩
随着合并的进行,分支的树形结构会变得越来越深,每次查找可能要多次递归才能找到树的根节点。最好的情况就是每个节点的父节点直接就是根节点,查找一次就能成功找到,此时树的高度为2。
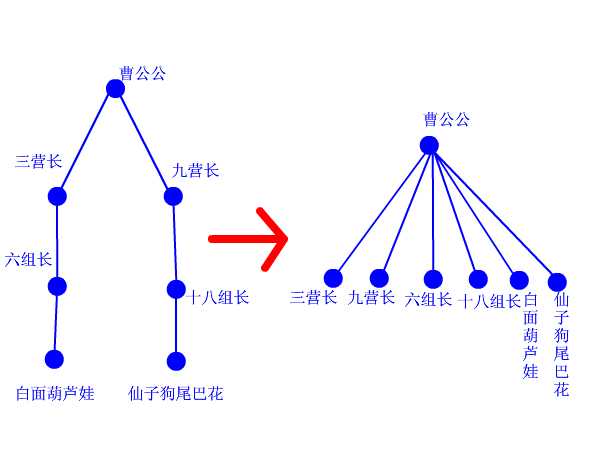
3.1 思路
每次查找x的代表时,让x到根节点的路径中的所有节点,都直接指向找到的根节点。
3.2 实现
int find(int x)
{
int r=x;
while(pre[r] != r) //一样的操作,查找根节点 r
r=pre[r];
int i=x , j ;
while(i != r)
{
j = pre[i]; //遍历x到根节点路径上的所有节点
pre[i]= r ; //直接指向根节点
i=j;
}
return r ;
}





